
Bhāskara II (1114 - 1185) was een Indiase wiskundige en astronoom.
Hij vond een eenvoudig bewijs voor de stelling van Pythagoras.
Hierop is deze knippuzzel gebaseerd.
Teken vijf gelijke rechthoekige driehoeken waarvan de ene rechthoekszijde dubbel zo lang is als de andere.
De puzzel bestaat erin de vijfde driehoek in twee stukjes te knippen
zodat je dan met de 6 puzzelstukken één groot vierkant kunt vormen.
Tips voor de oplossing.
Als de rechthoekszijden van elke driehoek lengte a en 2a hebben,
hoe lang is dan de schuine zijde van elke driehoek.
Wat is de totale oppervlakte van de 5 driehoeken samen
en hoe lang is bijgevolg de zijde van het te vormen vierkant?
Hieronder vind je de oplossing van de puzzel
en een algebraïsche versie van het bewijs van Bhāskara
voor de stelling van Pythagoras.
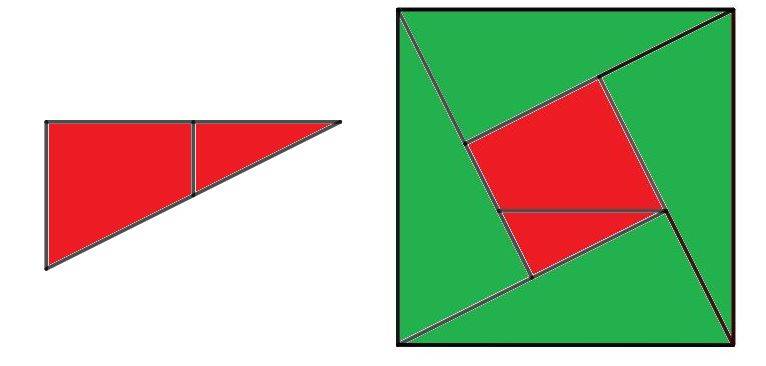
De rode rechthoekige driehoek wordt in twee stukken geknipt langs het lijnstuk dat het midden van twee zijden verbindt. Waarom kan je dan met die 2 puzzelstukjes het passende kleine vierkant vormen?

Maak jouw eigen website met JouwWeb